Kategori: NV09FMT

Kategori för alla inlägg i matematik och fysik rörande klass NV09FMT.

Vecka 3 – 4: Introduktion till Fysik A och Densitet

Fysik A - NV09FMTVälkommen till kursen Fysik A!

Under denna period kommer vi att att behandla prefix, SI-enheter (och omvandling mellan dessa), värdesiffror och densitet. Om detta står att läsa på sidorna 13 – 23 i Nexus A.

Du kommer att märka att vi använder oss av en del matematik i fysiken. Men fysik är inte matematik. Matematiken innebär till stor del logik och abstrakta resonemang kring tal som inte har någon koppling till den fysiska världen, medan fysiken utgår från den fysiska världen. Sedan förklaras och förutsägs den fysiska världen med hjälp av matematiken. Fortsätt läsa ”Vecka 3 – 4: Introduktion till Fysik A och Densitet”

Planering v. 48 – 50

Matematik A - NV09FMTFör utskriftsvänlig version, ladda ned här.

Vecka 47: Statistisk undersökning

Matematik A - NV09FMTDenna vecka avslutar vi teorin på statistikavsnittet och startar upp den undersökning som ska redovisas nästa vecka. De rekommenderade uppgifterna är redovisade i förra veckans blogginlägg; några nya uppgifter i boken tillkommer inte denna vecka. Istället finns den statistikuppgift som är aktuell här. Redovisning tisdag nästa vecka.

Vecka 45 och start v. 46: Funktioner uttryckt som matematiska samband

Matematik A - NV09FMTEfter träning på hur funktioner tolkas grafiskt, ska vi nu koppla ihop det tidigare genomgångna avsnittet om samband (formler) för att uttrycka funktioner med hjälp av dessa. Det du som elev förväntas kunna efter detta avsnitt är följande:

Vecka 43: Introduktion till funktioner

Matematik A - NV09FMTNu stundar snart höstlovet. Nu på tisdag är det prov, hoppas att alla kommer ihåg att vi byter sal till 4210 och att vi börjar kl. 8.00 den dagen (kompensation utlovas vid ett senare, överenskommet, tillfälle).
Jag tänker att vi på torsdag ska ha hunnit klart med inledningen till funktionsavsnittet. Det handlar i princip om koordinatsystem och tolkning av grafer. På fredag tänkte jag mig något trevligt mattespel eller liknande.
Rekommenderade uppgifter denna vecka: Fortsätt läsa ”Vecka 43: Introduktion till funktioner”

Vecka 42: Repetition och fördjupning

Matematik A - NV09FMTDenna vecka ägnar vi helt åt finslipning av de matematiska kunskaperna inför provet nästa vecka. Provet kommer att vara på Kapitel 2 och 3, dvs det kommer att behandla algebra, formler, ekvationslösning och procenträkning.

En vanlig uppfattning är att man är klar med en uppgift när man fått fram ett svar. Ett av målen denna vecka är att titta på kvaliteten på de svar man fått fram. Det är kvaliteterna som så småningom kommer att bedömas vid betygssättning, inte bara svaren.

Vidare kommer vi att gå igenom utvalda funktioner på Casio-räknaren samt hinna med några redovisningsuppgifter på lektion. Se planeringen nedan! Fortsätt läsa ”Vecka 42: Repetition och fördjupning”

Vecka 41: Procentenheter och index

Matematik A - NV09FMTVeckans uppgifter i Origo AB

Tisdag: 3138, 3140, 3142, 3143, 3144, 3145, 3147, 3201, 3203, 3204, 3206, 3208, 3209,3212, 3214, 3215, 3216
Onsdag: Procentaktivitet
Torsdag: 3217, 3218, 3220, 3222, 3223, 3224, 3226, 3227
Fredag: Blandade uppgifter: Eget urval av uppgifter på sidorna 106, 107.

Denna vecka tar vi upp två viktiga begrepp som har med procenträkning att göra. Det ena är procentenheter (sid. 95 i Origo AB) och det andra är index (sid. 97 i Origo).

Procentenheter förväxlas ofta med procent i media. Mitt favoriexempel som har med procentenheter att göra gäller sympatier för politiska partier. Säg att Parti X har en andel sympatisörer som är 20%. Något händer, och andelen sjunker plötsligt till 10%. Andelen sympatisörer har sjunkit med 10 procentenheter. Man kan även säga att andelen sympatisörer har sjunkit med 50% (antalet har ju halverats). Så procent och procentenheter är uppenbarligen inte samma sak. Fortsätt läsa ”Vecka 41: Procentenheter och index”

Vecka 40: Problemlösning och procent!

Matematik A - NV09FMTVeckans uppgifter i Origo AB

 

 

Tisdag: Halvklass förmiddagen med separat övning. Eftermiddagens lektion ägnar vi åt avsnitten Blandade uppgifter och Undersökningar.
Onsdag: Problemlösning i grupp med redovisningar
Torsdag: 3101, 3102, 3104, 3106, 3107, 3108, 3111, 3113, 3114, 3115, 3116, 3118
Fredag: 3119, 3120, 3122, 3124, 3125, 3127, 3129, 3130, 3131, 3133, 3135, 3137

Denna vecka befäster vi kunskaperna om algebra genom att arbeta med några alternativa övningar i början av veckan. Många har ju sett hur man t ex kan ”räkna ut” sin skostorlek ur diverse märkliga på ett närmast magiskt sätt. Denna veckas övningar syftar bl a till att punktera denna magi (en trollkarl avslöjar aldrig sina hemligheter, men detta är inte magi på Hogwart, utan matematik på Åva;)).

Vi kommer sedan in på grundläggande procenträkning, där vi också tar upp begreppen promille och ppm (parts per million). Jag hoppas, och tror, att omvandling mellan procentform (och promille och möjligen också ppm) är ”gammal skåpmat”; läs om det på sid. 88 i Origo.

Procentuella förändringar är ett huvudnummer i Matematik A, läs om dessa på sid. 91. Begreppet förändringsfaktor ska du känna dig bekväm med, det kommer att dyka upp många gånger under din tid på NV-programmet.

Vecka 39: Formler

Matematik A - NV09FMTVeckas uppgifter i Origo AB

 

 

Tisdag: 2301, 2302, 2304, 2305, 2306, 2308, 2310, 2311, 2312, 2313, 2315, 2316, 2319, 2321,
Onsdag: Arbete med Blandade uppgifter, Kapitel 2.
Torsdag: Matematiklektionen utgår pga Livskunskap
Fredag: Matematiklektionen utgår pga idrottsdag

Veckans avsnitt handlar om formler. Egentligen tycker jag inte om ordet formel för att det kanske för tankarna till magi. Magi är visserligen spännande, men matematik och magi hör inte ihop! Ett bättre ord är samband.

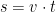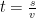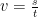Jag tar ett exempel: Ett samband mellan sträcka (s), tid (t) och hastighet (v) lyder s=v\cdot t. Detta kan skrivas om så att tiden eller hastigheten kan beräknas enligt t=\frac{s}{v} och v=\frac{s}{t}. Detta är alltså tre varianter på sambandet mellan sträcka, tid och hastighet eller, om man så vill, tre formler (vi säger att s, v och t är utlösta.

Du kommer att ha stor nytta av att kunna lösa ut storheter (t ex tid) ur ett samband. Att lösa ut något ur ett samband följer samma principer som ekvationslösning.

En viktig typ av samband är s.k rekursiva samband (se sid. 77 i Origo). Dessa används t ex om man har en talföljd eller ett mönster som man vill beskriva. Fördelen med de rekursiva sambanden är ofta att de ofta är enklare att konstruera för en given situation än de slutna sambanden (som är ”motsatsen” till rekursiva samband). Ett välkänt exempel på en rekursiv talföljd är Fibonaccis talföljd (se uppgift 2319 samt denna artikel på Wikipedia).

Vecka 38: Ekvationslösning

Matematik A - NV09FMTVeckas uppgifter i Origo AB

 

 

Tisdag: 2141, 2143, 2144, 2145, 2146, 2147, 2150, 2151, 2153, 2154, 2156, 2157, 2158
Onsdag: 2211, 2213, 2215, 2216, 2217, 2218, 2220, 2222, 2223
Torsdag: 2224, 2226, 2228, 2229, 2230, 2232, 2234, 236, 2237, 2239, 2243, 2247
Fredag: 2265, 2267, 2268, 2269, 2272, 2273, 2275, 2276, 2277, 2278, 2279, 2280 samt Diskutera och fundera

Denna veckas tema är ekvationslösning. Ordet ekvation betyder likhet, och har att göra med att man ska bestämma ett okänt tal, t ex som betecknas x, så att vänsterledet och högerledet ska bli lika. Exempel på ekvation.

2x+5=3x (Exempel på lineär ekvation) Fortsätt läsa ”Vecka 38: Ekvationslösning”