Att multiplikation kan ses som en upprepad addition med heltal lär vi oss tidigt i skolan. Det är ju för övrigt ganska häftigt att t ex \(4\cdot 3=4+4+4=3+3+3+3\). Det fungerar ju bra för heltal, men hur blir det med produkten av andra tal än heltal – vad betyder egentligen t ex \(\sqrt{2}\cdot{\sqrt{3}}\)? Här fungerar det ju inte med upprepad addition!
Vi lär oss också att produkter kan åskådliggöras som en ytas area. Här kan t ex arean vara \(\sqrt{6}\,\mathrm{ cm}^2\), men vad är egentligen en area för något? Ett mätetal för ytans storlek, som i sin tur alltså kan ses som en produkt. Observera att enheten som arean mäts i är längdenheten i kvadrat.
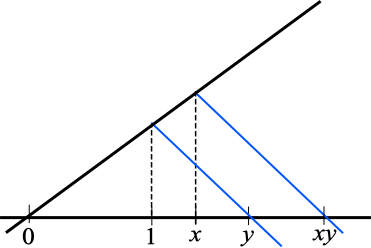
Ett alternativt sätt att åskådliggöra en produkt är med följande figur:
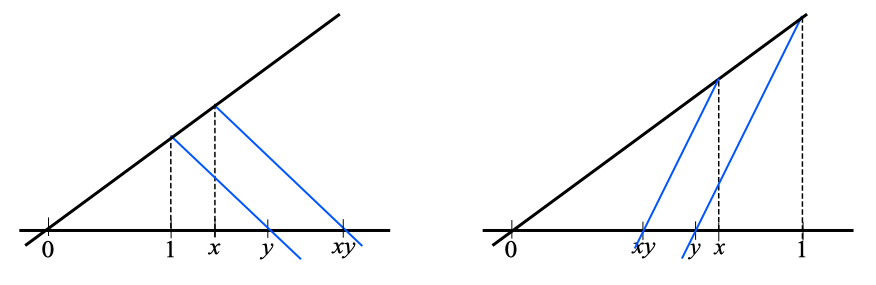
Observera ettans position, figuren till vänster visar multiplikation med två tal större än 1 och i figuren till höger är talen mindre än ett. Det är en modell som gör att produktens värde syns direkt på tallinjen. Det spelar heller ingen roll om det är heltal, rationella eller irrationella tal. Jag tycker det är en snygg representation som i vissa fall säger mer än en ytas storlek.
Varför funkar den här modellen? Det bygger på likformighet:

Jag tycker det är en vacker förklaring som, kanske, ger en förklaring till vad egentligen produkten av \(\sqrt{2}\cdot{\sqrt{3}}\) står för.