Introduktionen till differentialekvationer i Ma5 klar. Tänkt att vara en översikt av vad en differentialekvation är och innebörden av dess lösningar. Så fick jag ju koda lite också, både Python (för graferna) och CSS (för presentationen) 🙂
Etikett: differentialekvationer
Numeriska lösningar till differentialekvationer i Python
För att orientera mig om hur differentialekvationer kan lösas numeriskt i Python gjorde jag ett Jupyter-dokument som tar upp och löser flera av de typer av ordinära differentialekvationer som kommer upp i gymnasiets matematik- och fysikkurser. Dokumentet blir inte så bra att föra över i WordPress-miljö, så jag har lagt det här istället.
Jag använder mig av funktionen odeint() som finns i biblioteket SciPy. Funktionen genererar listor med godtycklig noggrannhet som sedan kan plottas. I dokumentet har jag beskrivit hur man går tillväga.
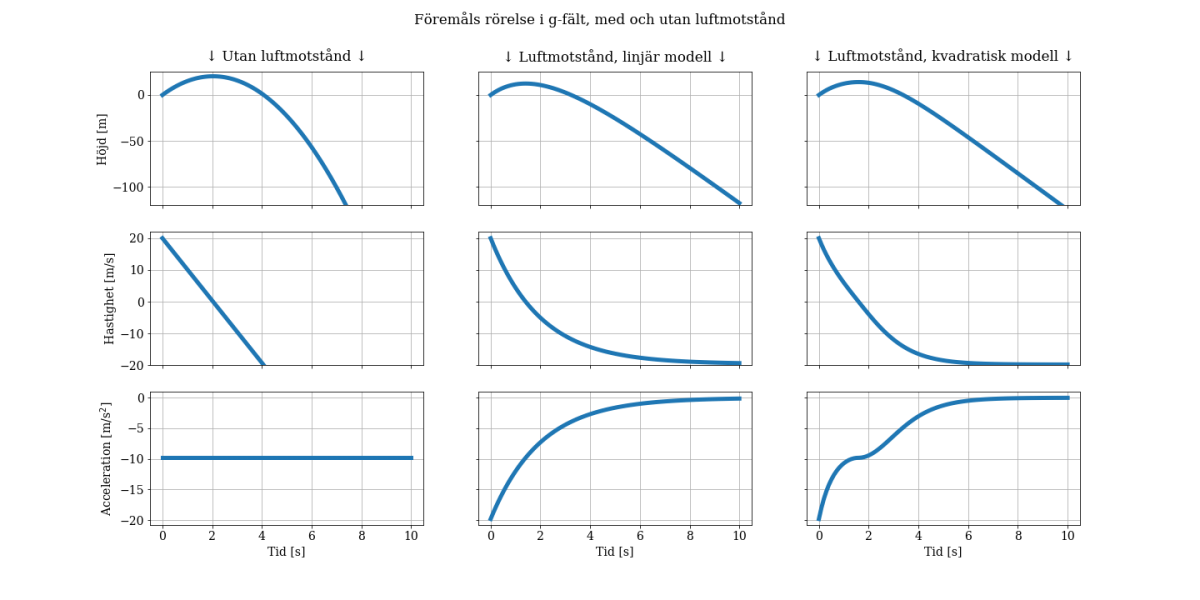
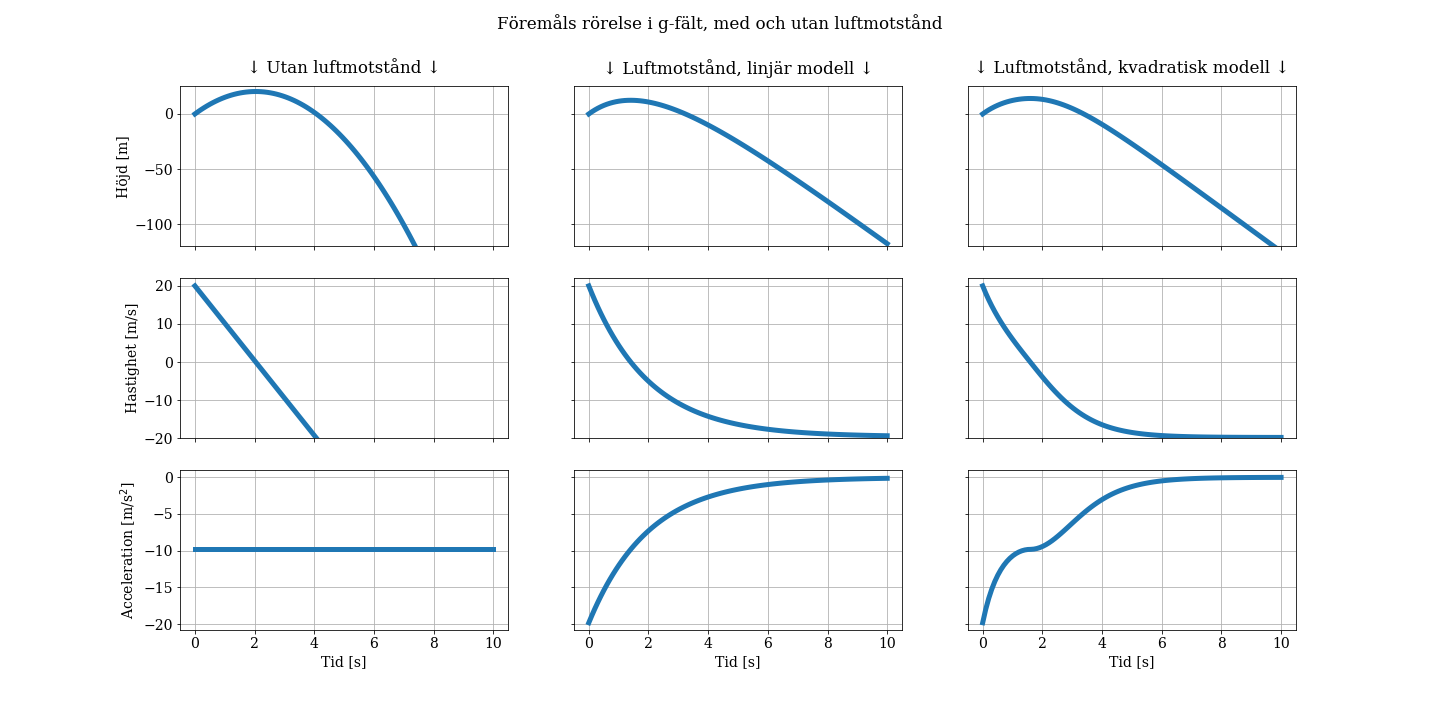
En av de grafer jag genererade var följande, som beskriver ett föremåls fall i gravitationsfältet enligt olika modeller med luftmotstånd.
Jag hoppas att dokumentet kan inspirera någon eller att det på något annat sett kommer till nytta!
Lektioner vecka 40 och 41: Differentialekvationer
Tidsplan för detta avsnitt (del av 3.3, sidorna 149 – 151, i Matematik 4000)
Torsdagen den 1/10 och måndagen den 5/10
Rekommenderade uppgifter
Alla på sid. 149 – 151.
Differentialekvationer
I en ”vanlig” ekvation är det ett tal som söks. Vi har en uppsätting regler för hur vi kan lösa ekvationer, och vi kan pröva, genom att sätta in lösningen i ursprungsekvationen, om den är giltig. I en differentialekvation är det inte ett tal som är det obekanta; det är en funktion. Fortsätt läsa ”Lektioner vecka 40 och 41: Differentialekvationer”