Problem med popcorn

Det kom fråga: Om en full strut rymmer två liter popcorn, hur mycket popcorn finns det i struten då den är fylld till två tredjedelar av höjden?

Embed from Getty Images

Det är en mycket bra fråga! Finns varianter av denna i matematikböcker både på högstadiet och gymnasiet. Och tro mig: även om den går fort att lösa bara på någon rad så involverar den ett koncept som många inte tycker är så enkelt.

En vanlig, men inte så effektiv, approach är att anta ett värde på höjden och att därefter beräkna basradien i konens topp. Därefter, kan man tänka sig, så beräknas basradien på den höjd som motsvarar två tredjedelar av hela konens höjd. Slutligen så beräknas volymen.

Som jag ser det finns det minst två problem med ovanstående approach: dels så blir det många steg och dels så har man just antagit ett värde på höjden. Krasst sett vet vi ju då inte om vi får samma volym på motsvarande höjd oavsett utformning på den konformiga struten!

Konceptet jag skulle använda här är volymskala, här innebär det att volymen är proportionell mot höjden i kubik. Volymen i en kon, med radien \(r\) och höjden \(h\) är

$$\displaystyle V_\text{Kon}=\frac{\pi r^2 h}{3}\tag{1}$$

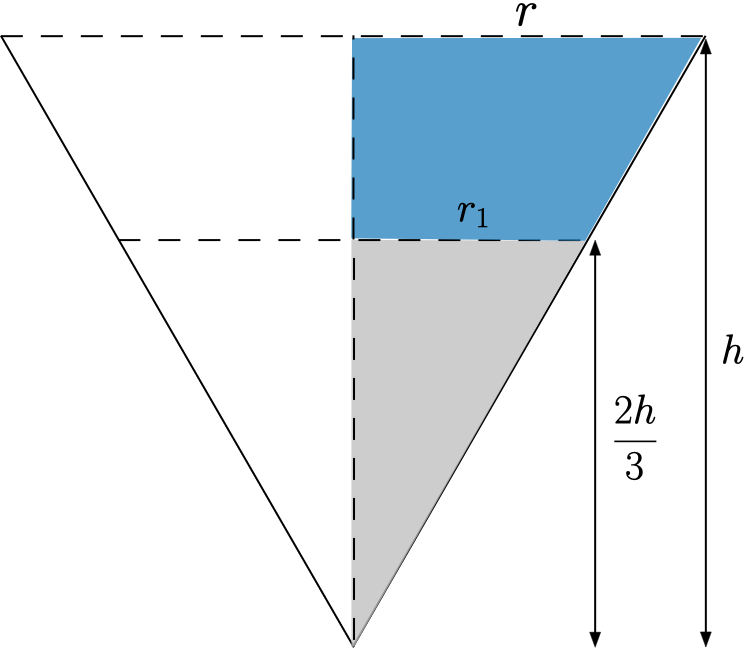
Proportionaliteten grundar sig i likformighet, som här kan åskådliggöras som likformiga trianglar. I nedanstående figur är den triangel som är färgad grå och blå, likformig med den grå triangeln. Det betyder att deras vinklar parvis är lika stora och att sidornas längder parvis står i samma förhållande till varandra. Figuren är ett tvärsnitt av struten; alltså som den ser ut om den syns från sidan. Detta används, och vi får sambandet

$$\frac{r}{r_1}=\frac{h}{\frac{2h}{3}}\Rightarrow \frac{r_1}{r}=\frac{2}{3}\Rightarrow r_1=\frac{2r}{3}\tag{2}$$

Om vi nu tar förhållandet mellan volymerna av den delfyllda och helfyllda konen så får vi efter lite algebraiska förenklingar där samband (1) används såväl som resultatet i (2).

$$\displaystyle\frac{V_\text{Delfylld kon}}{V_\text{Helfylld kon}}=\frac{2}{3}\cdot\frac{r_1^2}{r^2}=\frac{2}{3}\cdot\left(\frac{2}{3}\right)^2=\left(\frac{2}{3}\right)^3=\frac{8}{27}\tag{3}$$

Vi ser alltså att volymerna förhåller sig till varandra som höjderna i kubik. Multipliceras den fyllda konens volym (2 liter) med detta förhållande erhålls den eftersöka volymen som

$$\displaystyle2\cdot \frac{8}{27}=\frac{16}{27}=0.59\text{ liter}$$

Nu är volymen beräknad efter konstens alla regler! En genväg är just hågkomsten att volymen är proportionell mot höjden i kubik. Detta gäller alla kroppar där både längden och bredden förändras i likformigt med höjden och både längden och bredden är noll då höjden är noll. Det är det som är själva proportionaliteten.

Ett annat, lite mer grundläggande exempel, på användning av volymskala skulle kunna vara på kuber. Om alla sidor på en kub fördubblades, med hur många gånger skulle volymen öka då? Volymen kommer att bli åtta gånger så stor som den ursprungliga kuben, just därför att alla sidor ”hänger med” i förändringen. Det blir alltså en ökning med \(2^3=8\) gånger. Om enbart längden hade fördubblats (då har vi inte en kub längre) hade ökningen av volym blivit \(2^1=2\) gånger. Om både längd och bredd hade fördubblats hade volymen istället blivit \(2^2=4\) gånger så stor. Och om alla sidor förlängs till det dubbla så är ökningen av volymen som sagt \(2^3=8\) gånger.

Nu är du som har läst detta värd en strut med popcorn 😊