Under förra veckan blev jag intervjuad av en lärarstudent som snart är färdig med kombinationsutbildningen civilingenjör / lärare. Det gällde programmering i matematikundervisningen; för några år sedan så infördes detta i ämnesplanen för några matematikkurser på gymnasiet. Det blev ett utmärkt tillfälle för mig att strukturera mina egna tankar.
Fortsätt läsa ”Om programmering i matematikundervisningen”Författare: magistern
Veckans kluring, 2020-08
Denna kluring är ett problem taget från Kängurutävlingen 2016.
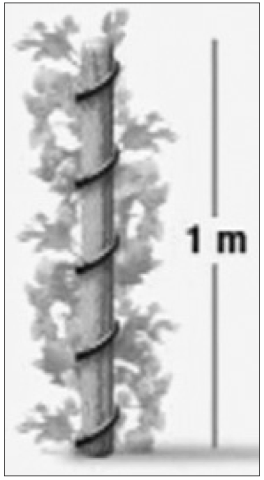
En växt slingrar sig exakt fem varv kring en stolpe som har höjden 1 m och omkretsen 15 cm. Varje varv slingrar sig växten lika lång sträcka i höjdled. Hur lång är växten?
Fortsätt läsa ”Veckans kluring, 2020-08”Vilken slutsiffra har talet?
I kursen matematik 5 går vi igenom moduloräkning, det är när man beräknar vilken rest två tal ger vid division med varandra. Man säger att två tal, säg \(a\) och \(b\), är kongruenta med varandra modulo ett annat tal, säg \(c\) om \(a\) och \(b\) ger samma rest när de divideras med \(c\). Nedan finns den presentation som jag använder i avsnittet.
Nå, i detta inlägg tänker jag inte gå igenom själva teorin; det är mest några uppgifter jag gav som sammanfattar en del av avsnittet. Inga digitala hjälpmedel!
- Vilken siffra slutar talet \(2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13 \cdot 17 \) på?
- Vilken siffra slutar talet \(12^{32}\) på?
- Vilken siffra slutar talet \(9^{101}\) på?
Reflektioner: Jag tänkte mig att den första uppgiften skulle bli någorlunda enkel för eleverna. Jag sa t o m att det skulle kunna vara en kluring för högstadieelever (jag hoppas att det stämmer!). Men jag tror att det var alla kongruensregler vi gått igenom som gjorde att många missade att tänka på vad faktorn 2 och 5 gör när de multipliceras med varandra.
Inför de övriga uppgifterna fick jag tipsa om att räkna modulo 10. Uppgift 2 är då en klassisk kongruensräkningsuppgift i flera steg som vi tränat på, medan uppgift 3 blir väldigt kort att beräkna eftersom man kan se 9 som kongruent med -1 då man räknar modulo 10.
Jag upplevde det som att det blev en bra repetition som gav mycket för eleverna.
Veckans kluring, 2020-07
Sultanen i Bengazien hade två favoritnöjen: kluriga logiska gåtor samt sadistiska lekar med de politiskamotståndare han spärrat i fängelse. Så en dag bestämde han sig för att kombinera båda.
”Jag väljer ut en fånge, ställer honom framför två dörrar och tvingar honom välja dörr. Bakom någon av dörrarna har jag låtit en hungrig tiger vänta. Ovanför dörrarna har jag satt upp skyltar med litet upplysningar. Om fången kan resonera logiskt och tolkar informationen rätt så att han väljer rätt dörr, utan någon tiger bakom, får han gå fri, annars …”

Sultanen satte tre fångar på prov. Alla tre fick veta att det kunde finnas en tiger bakom en av dörrarna, men det kunde också tänkas att det väntade tigrar bakom båda dörrarna, eller att det inte fanns någon tiger alls.
Och vad göra, om det väntar tigrar bakom båda dörrarna? — undrade den första fången missmodigt.
– Då har du otur, får man väl säga … — svarade sultanen.
– Och om det inte finns någon tiger alls, betyder det verkligen att jag blir fri?
– Jajamän!
– Men, om det finns tiger bakom en av dörrarna endast?
– Ja, då spelar det verkligen roll vilken dörr du väljer — det förstår du väl?!
– Hur skulle jag då kunna veta vilken jag ska välja?
Sultanen pekade då på skyltarna ovanför respektive dörr

och sade:
– En av skyltarna är sann, medan den andra är falsk. Men vilken som är vilken får du lista ut själv!
Denna fången klarade sig. Nu är det din tur 😏
Fortsätt läsa ”Veckans kluring, 2020-07”Veckans kluring, 2020-06
Hur gamla är dina barn?

Brevbäraren Barbro kom till ett hus där det visade sig att hon kände adressaten Mats sedan skoltiden. Det blev ett glatt återseende, och Barbro fick reda på att Mats nu har tre barn.
– Hur gamla är de? frågade Barbro.
– Produkten av deras åldrar är 36 år, sa Mats.
– Men jag måste veta något mer för att kunna beräkna åldrarna!
– Ja, summan av deras åldrar är detsamma som vårt husnummer.
Barbro gjorde några beräkningar. Slutligen sa hon:
– Du måste ge mig en ledtråd till.
– Ja, det har du rätt i. Den äldsta har just börjat spela piano.
Det gjorde att Barbro kunde beräkna åldrarna. Kan du?
Numeriska lösningar till differentialekvationer i Python
För att orientera mig om hur differentialekvationer kan lösas numeriskt i Python gjorde jag ett Jupyter-dokument som tar upp och löser flera av de typer av ordinära differentialekvationer som kommer upp i gymnasiets matematik- och fysikkurser. Dokumentet blir inte så bra att föra över i WordPress-miljö, så jag har lagt det här istället.
Jag använder mig av funktionen odeint() som finns i biblioteket SciPy. Funktionen genererar listor med godtycklig noggrannhet som sedan kan plottas. I dokumentet har jag beskrivit hur man går tillväga.
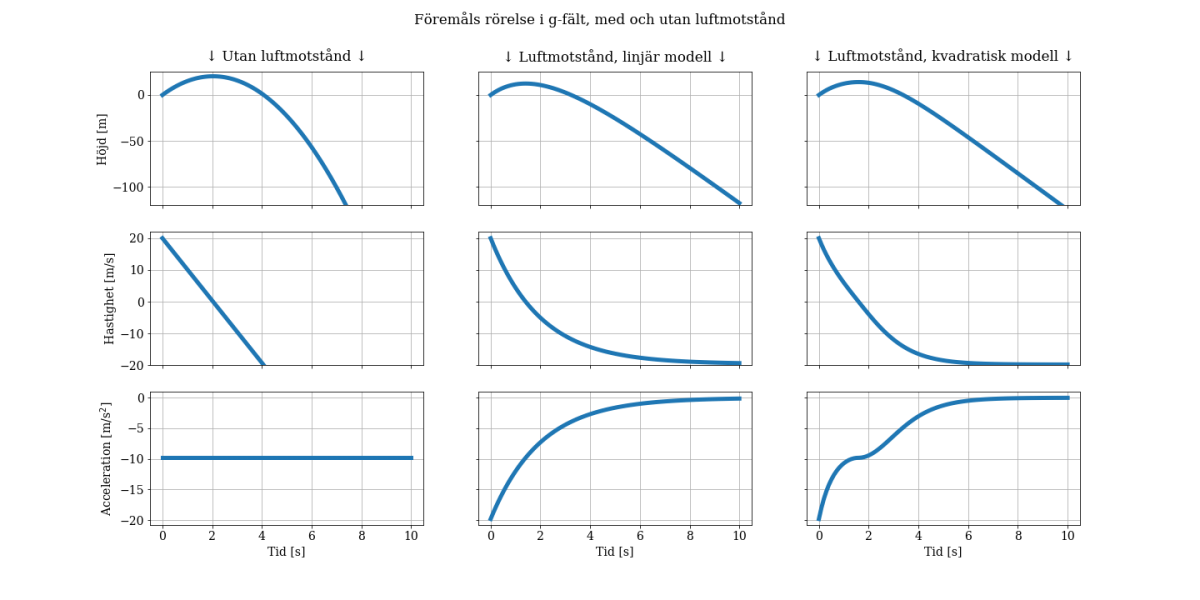
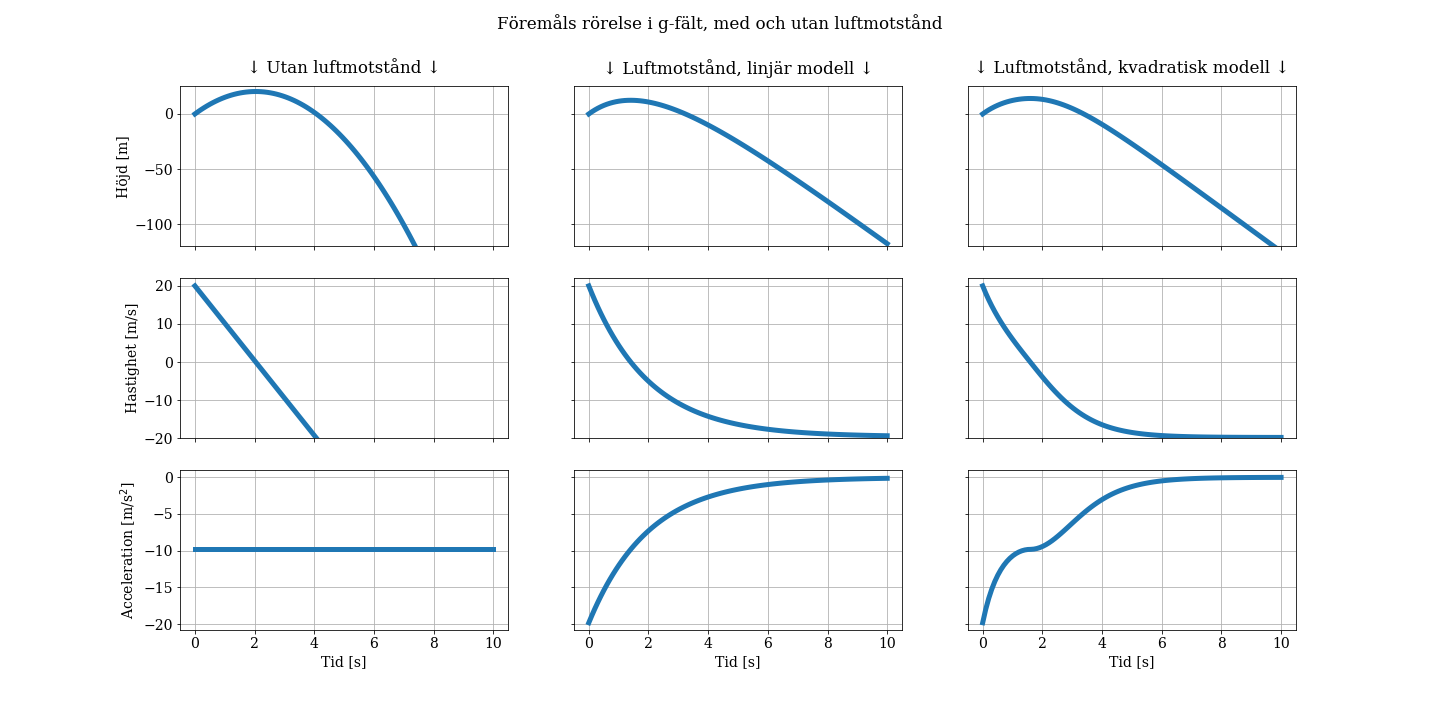
En av de grafer jag genererade var följande, som beskriver ett föremåls fall i gravitationsfältet enligt olika modeller med luftmotstånd.
Jag hoppas att dokumentet kan inspirera någon eller att det på något annat sett kommer till nytta!
Besök på CERN och ETH
Jag fick möjlighet att med skolan och tillsammans med en klass vara med på studiebesök på bl a CERN (det är de som har byggt en känd partikelaccelerator som bl a låg till grund för att den omtalade Higgs-partikeln bekräftades år 2013) och ETH (Zürich tekniska högskola).
På CERN fick vi dels träffa forskaren Richard Jacobsson som berättade om hur partikelfysiken ligger till grund Big Bang-teorin och dels fick vi en guidning runt den detektor som heter CMS, Compact Muon Solenoid.
Tredelning av cirkelns area med två linjer
Cirkelns geometri gör att det inte alltid blir helt lätt att avgöra hur stor andel som är utskuren. Skulle man t ex dela på en pizza på tre så är jag rädd för att de som fått den gula delen i bilden nedan kommer att känna sig förfördelad. Dessutom är det en större andel kant i ytterdelarna, så snitten kanske behöver läggas ytterligare in mot mitten för ultimat rättvisa.
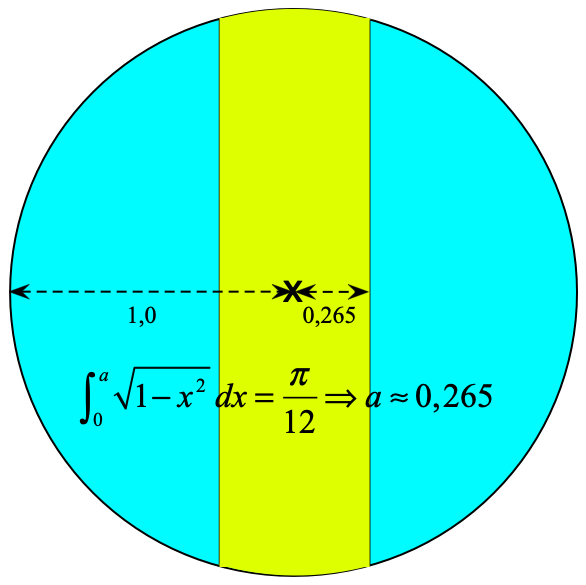
Lösningen på problemet är nog att beställa en större pizza. Om pizzans diameter ökar från 30 cm till 35 cm ökar dess area med 36 %.
För den som vill evaluera integralen i bilden ovan analytiskt så finns substitutionen som måste göras här.
Thomaes funktion – en riktig hjärnvrängare
Jag läser om Thomaes funktion. Det är en funktion som är diskontinuerlig överallt utom i de irrationella talen. Jag var inte bekant med funktionen sedan mina tidigare studier (inte vad jag minns, iallafall), och det visade sig bli en tillfredsställande bekantskap. Den går ut på att när man stoppar in ett rationellt tal i funktionen så får den ett värde som är skilt från noll. Stoppar man däremot in ett irrationellt tal så är funktionsvärdet definierat till noll. Sedan låter man funktionen operera på hela mängden av rationella tal. En del av resultatet syns i nedanstående bildserie.
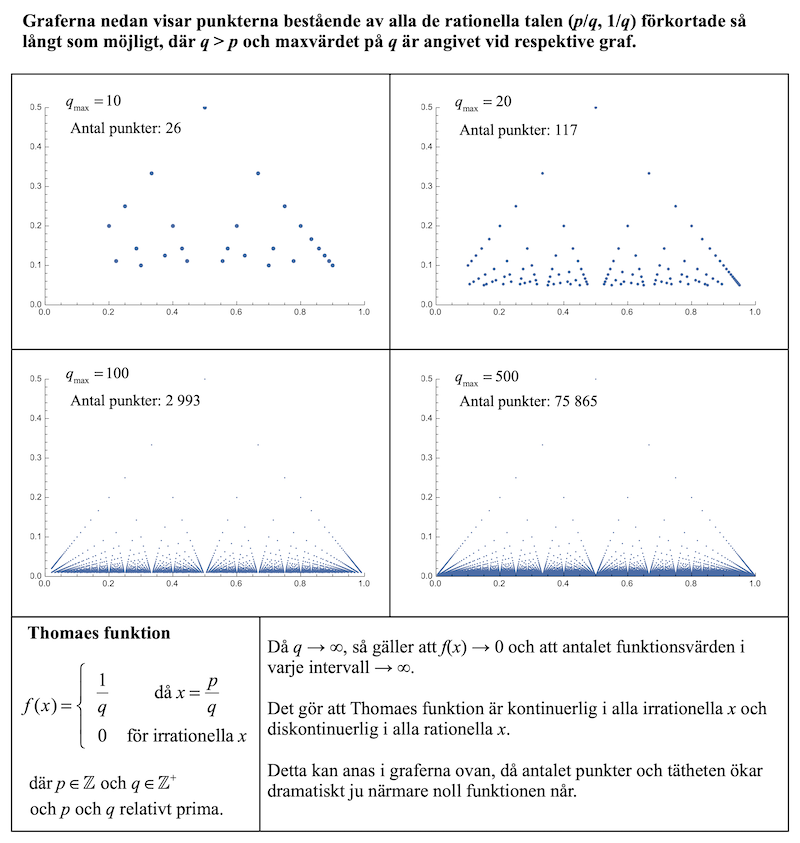
Kod i Mathematica (som är snodd härifrån); denna genererar ovanstående bilder:
maxq = 100;
fracs = Table[p/q, {q, 2, maxq}, {p, 2, q}] // Flatten //
DeleteDuplicates;
pq = {#, 1/Denominator@#} & /@ fracs;
ListPlot[pq, PlotRange -> {{0, 1}}]Kan man inte få nog av märkliga funktioner så rekommenderar jag att läsa om Dirichlets funktion, som faktiskt inte är kontinuerlig någonstans, eller Weierstrass funktion som är kontinuerlig överallt men som inte är deriverbar någonstans.
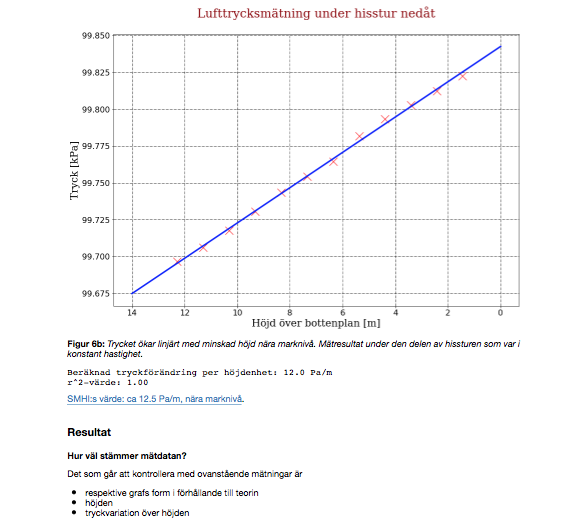
Ett his(s)keligt mätexperiment
Jag har gjort accelerations- och tryckmätningar i en hiss med hjälp av sensorerna i en mobiltelefon och åskådliggjort resultatet med Python och Jupyter. Läs om undersökningarna och resultaten här.
I ett tidigare inlägg har jag visat hur accelerationssensorerna i en mobiltelefon kan användas för att åskådliggöra olika accelerationsförlopp. Jag har nu byggt vidare på detta genom att jag tog med mig mobilen på en hisstur och såg vad jag kunde få ut av såväl accelerations- och tryckdata. Det blev mer, och bättre, än vad jag hade väntat mig. För att redovisa resultatet använde jag verktyget Jupyter, som är en webbaserad plattform för att köra Pythonkod och även för att visa grafer och bilder. Det blev som en typ av rapport.
Läs vad jag fick ut av det här, det är Jupyter-dokumentet i sin helhet.
För att anknyta till titeln, Ett his(s)keligt mätexperiment, så är nog själva Pythonkoden det enda hiskeliga. När jag idag publicerar detta var det mer än ett år sedan jag gjorde något med koden, och när jag tittar på den ser jag att jag skulle behöva flera timmar för att sätta mig in i den igen (och då kanske jag skulle gjort den på ett annat sätt). Som tur är är koden gömd i dokumentet, men den går att ta fram med hjälp av en knapp överst i dokumentet.