Jag fick möjlighet att med skolan och tillsammans med en klass vara med på studiebesök på bl a CERN (det är de som har byggt en känd partikelaccelerator som bl a låg till grund för att den omtalade Higgs-partikeln bekräftades år 2013) och ETH (Zürich tekniska högskola).
På CERN fick vi dels träffa forskaren Richard Jacobsson som berättade om hur partikelfysiken ligger till grund Big Bang-teorin och dels fick vi en guidning runt den detektor som heter CMS, Compact Muon Solenoid.
Visst är det långt till Månen, det kom figuren Månskådare på i den utmärkta filmen 2001. Det är 384 000 km, men vad är egentligen innebörden av detta? Jag roade mig med att göra ett par skalenliga bilder för att visualisera några avstånd i vårt solsystem.
Spontant så ligger det nära till hands att tro att det visserligen är långt, men att det faktiskt går att pressa in 30 jordklot i mellanrummet… det är mycket! Ändå ger Månen upphov till fenomen som tidvatten och solförmörkelser.
Avstånden mellan planeterna då?
Nu syns det knappt vad som står i bilden (klicka på den för en högupplöst version), men längst till vänster har vi solen. Därefter planeterna Merkurius, Venus, Jorden och Mars (och då förstår vi att avståndet från Jorden till Månen är ett bildligt stenkast i förhållande till våra närmaste planeter). Dessa planeter ligger tätt i förhållande till de yttre planeterna; Jupiter, Saturnus, Uranus och Neptunus, vars avstånd mellan varandra vida överstiger avståndet mellan Solen och Mars!
I ett uppföljande inlägg kommer jag att visualisera storlekarna på våra himlakroppar i solsystemet.
Dagens introduktion av en fysiklektion med en Teknikklass:
”En Tesla Model S P85D har data enligt nedan. Beräkna med hjälp av dessa hur snabbt bilen skulle kunna accelerera från 0 till 100 km/h. (Bortse från friktion och luftmotstånd.)”
Ledtrådar
Det blev en nyttig beräkning. Nu blev den beräknade accelerationstiden betydligt kortare än den som står i testprotokollet. Beror givetvis på verkliga förhållanden med luftmotstånd och friktion. Men det är ändå en nyttig beräkning i ett sammanhang som eleverna verkade uppskatta.
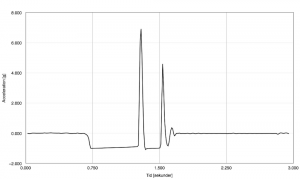
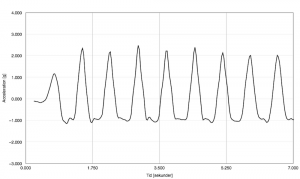
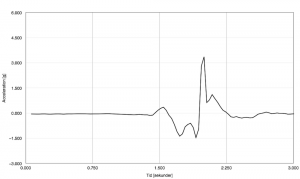
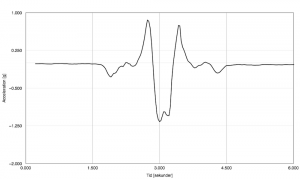
I gymnasiefysiken är ett av de centrala innehållen att kunna hantera mätvärden kvantitativt. Ett sätt att göra det på är att låta mätvärdena representeras i ett diagram, och utifrån grafen dra slutsatser och göra förutsägelser.
Min egen erfarenhet säger att det är lätt att spänna över ett kanske för stort område när jag har gjort övningar på detta. Det är någorlunda lätt att ta fram en laboration som ger mätvärden på t ex läget som funktion av tid, energi som funktion av temperatur eller spänning som funktion av ström.
I början av fysikstudierna blir det en ganska stor apparat för elever att hantera både laboration och en metod att hantera den data som laborationen ger; om flera steg ska göras i en följd är det vanligt att ett senare steg upplevs som väldigt mycket svårare jämfört med vad det skulle ha varit om detta steg gavs som ett separat problem.
Jag brukar numera försöka vara väldigt medveten om när jag gör vad och vilket syfte jag har med övningen ifråga, och delar nu med mig av två exempel som tränar centralt innehåll i såväl Fysikens karaktär, arbetssätt och matematiska metoder som Energi och energiresurser.
De båda exemplen nedan hoppas jag tränar en metod att hantera mätdata. Att sedan ta fram mätdata från en laboration är en annan sak, och målet är givetvis att elever lär sig att hantera data från sina egna mätningar.
Den 25 november år 1915 lade Albert Einstein fram en teori som så smått (eller stort) skulle chockera världen. Den allmänna relativitetsteorin beskriver hur tid och rum förändras vid olika gravitationer (visste du t ex att tiden för dina fötter skiljer sig från tiden för ditt huvud med knappt en miljondels sekund, räknat på en livstid?). Jag ska inte skriva så mycket mer om denna; det finns det andra som har gjort bra inför denna dag.
T ex har såväl tidningarna Dagens nyheter och Svenska dagbladet publicerat varsin artikel av varsin professor idag. Och allas vår Randall Munroe (xkcd.com) har skrivit en artikel (med de 10 000 vanligaste engelska orden) som ger en liten inblick i teorin.
Här är länkarna till artiklarna: Fortsätt läsa ”Grattis på 100-årsdagen, Allmänna relativitetsteorin”
Dagens moderna telefoner innehåller en mängd sensorer. Jag misstänker att många av dessa primärt är till för få en bra användarupplevelse under nyttjande av t ex spel. Det finns dock appar som kan extrahera rådatan från sensorerna, så att denna kan behandlas på valfritt sätt. Detta passar utmärkt i fysikundervisningen.
Jag gjorde själv några experiment där jag under några situationer mätte accelerationen med telefonen. Nedan finns mina genererade grafer. Jag kommenterar inte graferna, men konstaterar att vissa ser ut som ”skolexempel”, medan andra har lite egendomliga ojämnheter.
I samtliga fall är den positiva accelerationsriktningen uppåt, och ett fritt fall motsvarar accelerationen -1g.
På den gymnasieskola som jag är lärare på har vi under åren av och till diskuterat syftet med fysiklaborationer. Varför laborerar vi i fysik? Vad ska eleverna få ut av en laboration? Hur ska en laborationsredogörelse se ut? Hur ska redogörelserna bedömas?
Ett sätt att kanske hitta svar på frågorna är att titta på Skolverkets kursprov i fysik, där det också ingår en laborativ del. De är visserligen frivilliga att genomföra på skolorna, men jag tror att uppgiftstyperna kan ses som representativa för vad Skolverket avser med sina formuleringar i ämnesplanen. Där finns bl a följande relevanta punkter i det centrala innehållet: Fortsätt läsa ”Några tankar om laborationer i gymnasiets fysikundervisning”
All problemlösning i fysik utgår från någon eller några fysikaliska principer. Det kan t ex vara någon av Newtons rörelselagar, någon av termodynamikens huvudsatser eller någon av av de lagar som kan uttryckas med Maxwells ekvationer. En av gymnasiefysikens stora uppgifter är att eleverna ska lära sig anknyta vissa fysikaliska lagar till situationer, och därur kunna identifiera situationer och göra förutsägelser med hjälp av dessa. Ämnesplanen i gymnasiefysiken (Gy11) säger bl a att undervisningen ska ge eleverna förutsättningar att utveckla
Syftet med den här serien av blogginlägg – Fysikaliska principer – är att utifrån några exempel på olika teman försöka påvisa hur de grundläggande fysikaliska principerna används för att lösa fysikaliska problem genom att teckna de ekvationer som är relaterade till principerna. Målet är att få en stor spridning på problemen och att tydliggöra kopplingen till den aktuella fysikaliska principen. Idag inleder jag serien med några exempel som har att göra med termodynamikens första huvudsats, Energiprincipen.
Fortsätt läsa ”Fysikaliska principer, Del 1 – Energiprincipen”
