Centralrörelse och harmonisk svängningsrörelse

I detta inlägg finns en del teori, figurer och interaktiva demonstrationer som har med centralrörelse och harmonisk svängningsrörelse att göra.

Tidsplan

må. 21/3, on . 23/3, må. 28/3, on. 30/3, må. 4/4 , on. 6/4, må. 11/4 samt fr. 15/4 (prov)

Ingående teorimaterial

6.1, 6.2, 6.3, 6.4, 6.5 och 6.6 i Heureka! B
Dokumentet Centripetalkraft

Beträffande avsnittet 6.3 så gäller att du skall kunna använda dig av Newtons gravitationslag. Keplers lagar ingår inte.

Laborationer

Vi kommer att göra en laboration under avsnittet:

Kraftmätning i centralrörelse (Grupp 2: 25/4, Grupp 1: fr. 1/4)

Vi kommer även vid något tillfälle att arbeta laborativt i helklass

Rekommenderade uppgifter

6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7, 6.10, 6.11, 6.19, 6.20, 6.21, 6.23, 6.24, 6.26, 6.28, 6.30, 6.33, 6.34, 6.35, 6.38, 6.39, 6.41 och 6.42

Interaktiva demonstrationer

Till dessa demonstrationer behövs programmen Wolfram cdf-player och Java (Java brukar vara förinstallerat på datorer).

Alla ovanstående demonstrationer är det refererat och länkat till i rätt sammanhang i texten nedan, detta är en sammanställning.

Introduktion

Denna period kommer vi att behandla centralrörelse och harmonisk svängningsrörelse. Kanske det kan verka som att dessa delar inte har speciellt mycket med varandra att göra, men jag kommer att visa att de faktiskt hänger ihop!

Centralrörelse

En centralrörelse innebär att ett föremål kretsar runt ett centrum, t ex en karusell som snurrar runt sin axel (en punkt mitt i karusellen) eller då vagnen i en berg-och-dalbana färdas i en loop (då utgör en punkt mitt i loopen, i luften) banans centrum.

Ett föremål accelererar när det ändrar sin hastighet. I dagligt tal menar vi en fartökning utefter en rät linje, men begreppet hastighet omfattar ju även en riktning. Så strängt taget innebär alltså det att då ett föremål ändrar sin riktning, så undergår det en acceleration. I en centralrörelse sker en kontinuerlig riktningsändring, och därmed är det en kontinuerligt accelererad rörelse.

Vi känner även till Newtons andra lag, Kraftekvationen:

$F=ma$

För att upprätthålla en acceleration krävs en kraft. I dokumentet Centripetalkraft har jag motiverat denna krafts riktning in mot centrum med hjälp av en satellit som kretsar kring Jorden. Detta är ett exempel, men riktningen på centrietalkraften är alltid riktad in mot centrum. Ordet centripetalkraft betyder för övrigt centrumsökande kraft. Är det fråga om centripetalacceleration, så gäller att

$a_c=\frac{v^2}{r}$ .

Då

$F=ma$

och

$a_c=\frac{v^2}{r}$

gäller att centripetalkraften

$F_c=\frac{mv^2}{r}$ .

I dokumentet Centripetalkraft finns exempel på hur det sambandet skall användas samt en motivering till varför uttrycket ser ut som det gör.

Intuitivt kan det tyckas egendomligt att kraften är riktad inåt. I en karusell känner vi ju faktiskt av en kraft som är riktad utåt! Och om vi befinner oss högst uppe i en loop borde vi ju falla ned om en kraft påvekar oss mot centrum. Förklaringen till detta är föremålens tröghet. Åker vi i en bil som accelererar (ökar farten) rakt fram måste ju kraften vara riktad framåt; ändå känner vi att vi pressas bakåt. Det är ett helt jämförbart förhållande med centripetalaccelerationen. Kroppens tröghet innebär att den motverkar hastighetsförändringen. I fallet centralrörelse är kraften (och därmed accelerationen, hastighetsförändringen) riktad mot centrum, men kroppens motverkan gör att vi upplever det som att vi pressas utåt. Nedanstående figur på en roterande karusell, med krafter utritade på en av respektive gondol, kanske gör det hela mer tydligt.

Illustration hur centripetalkraften beror av rotationshastighet — Illustration över hur centripetalkraften beror av rotationshastighet. (Klicka på bilden för att komma till dess beskrivningssida med licensinformation)

De krafter som verkar på föremålet är tyngden nedåt (alltid!) och snörkraften riktad snett uppåt (kraften måste ha samma riktning som snöret och vara riktad åt det håll att den motverkar tyngdkraften i denna situation; annars skulle ju gondolen fallit ned). Beroende på riktningsskillnaden mellan dessa krafter kommer vi att få en resulterande kraft mot mitten – centripetalkraften. Centripetalkraften är den resulterande kraften på ett föremål som beskriver centralrörelse. Observera att centripetalkrafter aldrig verkar på föremålet (som alltid med resulterande krafter då det är fler än en kraft som verkar). Studera gärna denna Java-applet, och undersök vad som händer med centripetalkraften då rotationshastigheten förändras.

Centrifugalkraften är en s.k fiktiv kraft, som upplevs av en observatör inuti ett roterande system. Nedanstående YouTube-klipp visar en rotation både ur två perspektiv:

I Fysik B görs inte beräkningar med centrifugalkraft, men man bör känna till att den s.k centrifugalkraften har med tröghet, snarare än en kraft, att göra.

Period, frekvens och vinkelhastighet

I läroboken talas om periodtiden för en roterande rörelse. Det är den tid det tar för en punkt i en roterande rörelse att återkomma till ursprungsläget. Det talas också om vinkelhastighet, ω (uttalas ”omega”, en grekisk bokstav). Denna mäts i enheten 1 radian per sekund, där ett varv är 2π radianer. Slutligen finns också begreppet frekvens. Det är hur många varv ett roterande föremål snurrar på en sekund. Med hjälp av dessa storheter kan man skriva om uttrycket för centripetalacceleration på flera ekvivalenta sätt. Det är viktigt att du lär dig omvandla mellan periodtid, frekvens och vinkelhastighet. Detta finns på sid. 138 i Heureka! B.

Pendelrörelse, eller harmonisk svängningsrörelse

När vi startar upp detta avsnitt måste vi inleda med lite matematik: nämligen hur läget hos en roterande rörelse beskrivs med trigonometriska funktioner samt hur man ur ett föremåls läge vid respektive tidpunkt kan beräkna dess hastighet och acceleration. Detta har med derivata av de trigonometriska funktionerna att göra; jag kommer att hänvisa till rätt avsnitt i matematikboken Origo D i ett senare blogginlägg.

Inledningsvis nämndes att pendelrörelse och rotationsrörelse är besläktade med varandra, vilket motiverar att de hamnar i samma kapitel i läroboken. På sid. 147 i läroboken visas en bild där man projicerar skuggan av en roterande tändsticka samtidigt som man låter en tyngd svänga fram och åter i en fjäder. Hittas ett läge med rätt rotationshastighet samtidigt som fjädern släpps i rätt ögonblick, kommer tändstickans skugga och tyngden att svänga i fas. Läget i y-led hos en tyngd i en fjäder är detsamma som läget i y-led hos ett föremål som roterar vid en och samma tidpunkt (givet att rotationshastigheten är anpassad efter fjäderkonstanten). För dig som vill undersöka detta närmare finns denna Mathematica-demonstration att tillgå.

I och med att harmonisk svängningsrörelse kan beskrivas ur cirkulär rörelse, så innebär det att begreppen Periodtid, Frekvens och Vinkelhastighet är gångbara även för denna typ av rörelse. Periodtiden definieras som den tid det tar för ett föremål (i harmonisk svängningsrörelse) att komma tillbaka till samma vändläge.

Det som skapar en svängningsrörels är att det finns en kraft som verkar återställande mot ett jämviktsläge. I en harmonisk svängningsrörelse är denna krafts storlek proportionell mot avståndet till jämviktsläget. Detta gäller t ex fjäderpendlar (avsnitt 6.4 i läroboken) och ”matematiska pendlar”, som är en trådpendel med litet vinkelutslag (avsnitt 6.6 i läroboken).

För fjädrar beräknas den återställande kraften enligt Hookes lag. Här finns en Mathematica-demonstration för denna lag. En annan Mathematica-demonstration visar hur en pendelrörelse beskriver en sinuskurva.

Du har nog inte misslyckats med att bestämma mg, däremot kanske du har mätt omloppstiden fel och beräknat en centripetalkraft som avviker mot den verkliga. Man kvadrerar ju den tangentiella hastigheten (v), så ett sådant mätfel växer ju… Vidare är det viktens avstånd till rotationscentrum som ska mätas, där är det risk att det blir lite fel. Slutligen görs en del förenklingar, som måste göras (mer om det nedan). Jag vet inte riktigt vad uppgiften gick ut på, men det verkar som att du skulle bestämma centripetalkraften och dra någon slutsats kring denna i förhållande till övrigt kända data.

Den första förenklingen som görs är att (som du skriver i ovan). Det är omöjligt såväl i teorin som i praktiken, därför att det måste finnas en kraft uppåt som motverkar den snurrande viktens tyngd. Denna kraft utgörs av den vertikala komposanten till snörets spännkraft (se figurerna i artikeln ovan under bilderna på karusellen). Spännkraften i snöret kan som maximalt bli mg (nej, den blir större, men se andra förenklingen i näsa stycke!), där m är motviktens massa. Det skulle innebära att centripetalkraften egentligen är något mindre än tyngden på motvikten (i figuren under karusellbilden syns att $F_c<T$ (längden på kraftpilarna alltså, riktningarna skiljer sig såklart!). [se nästa kommentar för korrigering]

Den andra förenklingen som "måste" göras är att snöret glider friktionsfritt över glasrörets öppning. Tänker man sig tvärtom, en "maximal" friktion, så skulle denna nypa fast snöret i öppningen. Då skulle man kunna snurra runt i en väldigt hög fart och spänningen i snöret skulle bara bli större och större. Tänker man efter här måste denna friktionskraft vara riktad i snörets riktning nedåt (eftersom den håller emot draget utåt).

Centripetalkraften är riktad in mot rotationscentrum. Givet dessa båda förenklingar måste rotationscentrum vara i snörets riktning, alltså den del av snöret som roterar horisontellt. Den snurrande vikten påverkas bara av en kraft, nämligen snörspänningen (ja, i någon mån kan den liknas vid en normalkraft). Snörspänningen uppkommer av att en kraft förmedlas genom snöret. I det här fallet uppkommer spänningen av motviktens tyngd (man kan likna det med att dra i ett rep som sitter fast i en vägg, spänningen kommer att bli dragkraften även om väggen påverkar repet med lika stor kraft åt andra hållet – det blir alltså inte dubbla dragkraften). Alltså: $F_c=mg$ .

Den resulterande kraften du frågar om är just av de verkande krafterna (som i denna modell endast är en). Se bilder i artikeln ovan och i detta dokument (speciellt avsnitten 2.2 – 2.4). Oftast är de verkande krafterna tyngdkraft, normalkraft från underlaget, spännkraft från ett snöre, en elektrisk eller magnetisk kraft eller en friktionskraft. Beskriver ett föremål en cirkulär rörelse kallas den resulterande kraften (av t ex några av de ovanstående) för centripetalkraft.

Hoppas att detta hjälpte!

Svara

6 reaktioner till “Centralrörelse och harmonisk svängningsrörelse”

Fredrik skriver:

1 mars, 2013 kl. 12:27

Har nyligen gjort en labb på centralrörelse och är inte säker på att jag har förstått det riktigt. Hur är relationen mellan centripetal kraft, tyngdkraften, snörkraften?? Gjorde den klassiska labben men att trä ett snöre genom ett glasrör och sen har tyngder på var sida och sen snurra tyngden och se om den undre tyngden åker uppåt och radien på banan av den horisontellt flygande tyngden öka. Räknade ut centripetal kraften till 1,6N och tyngdkraften (allts den undre tyngden gånger gravitationen) var 0,8N. Är då snörkraften 0,8N? Är Fc=Fs+Fg? Sen blev jag lite osäker på riktningen av gravitationen, är den negativ?

Jag tänkte så här att om Fc=Fs+Fg (i mitt fall 1,6N=xN+0,8N) då borde jag väl uppnått jämvikt (dvs snöret rör sig inte upp eller ner)? Och det borde också betyda att mina mätresultat och beräkningar är tillförlitliga?

Tack för hjälpen!

Fred

Svara
Nikodemus Karlsson skriver:

10 mars, 2013 kl. 09:22

Hmm, som jag förstår det måste tyngden nedåt (som utgörs av motvikten) vara den enda kraften nedåt – eller hur? Och eftersom systemet är i vertikal jämvikt måste ju denna tyngd också vara det enda som ger upphov till spännkraften i snöret (det hade inte spelat någon roll om vi hade fäst snöret på något annat sätt än genom rotation, om du förstår hur jag menar).

Vidare är centripetalkraften den resulterande kraften i en rotation, och om vi bortser från friktionen i rörets mynning kommer den enda kraften i snöret att komma från tyngden nedåt – vilket alltså blir centripetalkraften.

Så i ditt fall blir gäller att $F_c=mg=F_s$ (med m som massan för motvikten), om jag förstått din aktuella uppställning korrekt.

Svara
1. Fredrik skriver:
  
  10 mars, 2013 kl. 15:55
  
  Så om jag då har räknat ut Fc till 1,6N och mg till 0,8N så har det blivit ganska galet i experimentet (dvs att med hjälp av omloppstiden räkna ut Fc)? det är ju svårt att misslyckas med mg, så fel kan man ju inte väga.
  
  Var jag har svårast att förstå är ju relationen mellan centripetalkraften, snörkraften (kan man kalla denna normalkraften?) och tyngdkraften. Jag har ju läst att cetripetalkraften är en resultantkraft, men resultanten av vad?
  
  Tack för hjälpen!
  
  Svara
  1. Nikodemus Karlsson skriver:
    
    10 mars, 2013 kl. 21:16
    
    Du har nog inte misslyckats med att bestämma mg, däremot kanske du har mätt omloppstiden fel och beräknat en centripetalkraft som avviker mot den verkliga. Man kvadrerar ju den tangentiella hastigheten (v), så ett sådant mätfel växer ju… Vidare är det viktens avstånd till rotationscentrum som ska mätas, där är det risk att det blir lite fel. Slutligen görs en del förenklingar, som måste göras (mer om det nedan). Jag vet inte riktigt vad uppgiften gick ut på, men det verkar som att du skulle bestämma centripetalkraften och dra någon slutsats kring denna i förhållande till övrigt kända data.
    
    Den första förenklingen som görs är att (som du skriver i ovan). Det är omöjligt såväl i teorin som i praktiken, därför att det måste finnas en kraft uppåt som motverkar den snurrande viktens tyngd. Denna kraft utgörs av den vertikala komposanten till snörets spännkraft (se figurerna i artikeln ovan under bilderna på karusellen). Spännkraften i snöret kan som maximalt bli mg (nej, den blir större, men se andra förenklingen i näsa stycke!), där m är motviktens massa. Det skulle innebära att centripetalkraften egentligen är något mindre än tyngden på motvikten (i figuren under karusellbilden syns att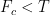 $F_c<T$ (längden på kraftpilarna alltså, riktningarna skiljer sig såklart!). [se nästa kommentar för korrigering]
    
    Den andra förenklingen som "måste" göras är att snöret glider friktionsfritt över glasrörets öppning. Tänker man sig tvärtom, en "maximal" friktion, så skulle denna nypa fast snöret i öppningen. Då skulle man kunna snurra runt i en väldigt hög fart och spänningen i snöret skulle bara bli större och större. Tänker man efter här måste denna friktionskraft vara riktad i snörets riktning nedåt (eftersom den håller emot draget utåt).
    
    Centripetalkraften är riktad in mot rotationscentrum. Givet dessa båda förenklingar måste rotationscentrum vara i snörets riktning, alltså den del av snöret som roterar horisontellt. Den snurrande vikten påverkas bara av en kraft, nämligen snörspänningen (ja, i någon mån kan den liknas vid en normalkraft). Snörspänningen uppkommer av att en kraft förmedlas genom snöret. I det här fallet uppkommer spänningen av motviktens tyngd (man kan likna det med att dra i ett rep som sitter fast i en vägg, spänningen kommer att bli dragkraften även om väggen påverkar repet med lika stor kraft åt andra hållet – det blir alltså inte dubbla dragkraften). Alltså: $F_c=mg$ .
    
    Den resulterande kraften du frågar om är just av de verkande krafterna (som i denna modell endast är en). Se bilder i artikeln ovan och i detta dokument (speciellt avsnitten 2.2 – 2.4). Oftast är de verkande krafterna tyngdkraft, normalkraft från underlaget, spännkraft från ett snöre, en elektrisk eller magnetisk kraft eller en friktionskraft. Beskriver ett föremål en cirkulär rörelse kallas den resulterande kraften (av t ex några av de ovanstående) för centripetalkraft.
    
    Hoppas att detta hjälpte!
    
    Svara
Nikodemus Karlsson skriver:

11 mars, 2013 kl. 07:57

Jag får nog korrigera mig själv lite på en punkt från mitt förra svar. Man bör inte göra förenklingen att snöret står vinkelrätt mot rotationscentrum, det kan det inte göra – och det var det jag avsåg när jag skrev att vikten inte kan rotera i horisontalplanet. Håller man däremot glasröret vertikalt kommer förstås vikten att rotera i horisontalplanet. Det man får tänka på då är också att avståndet till rotationscentrum inte går att mäta med snöret…

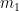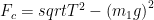Jag förstår din beskrivna uppställning precis som enligt karusellbilden ovan. De krafter den roterande vikten påverkas av är sin egen tyngd och spännkraften från snöret. Spännkraften T kommer från motvikten, och uppgår till motviktens tyngd. Om den roterande viktens massa är $m_1$ , så erhålls $F_c$ ur Pythagoras sats enligt $F_c=sqrt{T^2-{(m_1g)}^2}$ .

Detta ger en mindre centripetalkraft än den föregående, och det verkar inte vara ett bra resultat med tanke på vad du skriver. Det kan framför allt förklaras med att avståndet till rotationscentrum kanske inte är rätt uppmätt, att periodtiden för rotationen kanske inte är rätt och att spännkraften de facto är större än motviktens tyngd pga friktion från glasrörets kant.

Svara
Fredrik skriver:

11 mars, 2013 kl. 20:00

Stort tack for din hjälp och din tid! Verkligen uppskattat, förstår det mycket bättre nu!

Svara

Dela detta:

6 reaktioner till “Centralrörelse och harmonisk svängningsrörelse”

Kommentera gärna, markdown-formatering OK.Avbryt svar