Trigonometri i enhetscirkeln och i rätvinkliga trianglar

Trigonometri i trianglar

Ordet Trigonometri kommer från grekiskans ”trigōnon” (triangel) och ”metron” (mäta). Vi har tidigare studerat trigonometri trianglar, och sett att definitioner för de trigonometriska värdena sinus, cosinus och tangens, för en given vinkel, utifrån figuren nedan lyder:

Bild 1: Rätvinklig triangel med sidorna a, b, c och vinklarna A, B, C

Sinus	Cosinus	Tangens
$\sin A=\frac{a}{c}$	$\cos A=\frac{b}{c}$	$\tan A=\frac{a}{b}$
$\sin B=\frac{b}{c}$	$\cos B=\frac{a}{c}$	$\tan B=\frac{b}{a}$

Tabell 1: Definition av de trigonometriska funktionerna utifrån en rätvinklig triangel

Sidan a kallas katet (den är närliggande katet till vinkel B och motstående katet till vinkel A), sidan b kallas också katet (den är närliggande katet till vinkel A och motstående katet till vinkel B) medan sidan c kallas hypotenusa (den är motstående till den räta vinkeln i triangeln).
De trigonometriska värdena anger alltså förhållanden mellan olika sidor i triangeln. En viktig relation mellan sinus, cosinus och tangens för en vinkel v, som också erhålls ur Bild 1 ovan (hur?) är

$\tan v=\frac{\sin v}{cos v}$

Med hjälp av en liksidig triangel med sidan 1, där varje vinkel är 60° (varför är det så?) och en likbent rätvinklig triangel med de lika långa sidorna 1, så kan man ta fram några exakta värden för de trigonometriska funktionerna:

Bild 2: Trianglar för härledning av grundläggande trigonometriska värden

$\sin 30^\circ=\frac{1}{2}$	$\sin 45^\circ=\frac{1}{\sqrt 2}$	$\sin 60^\circ=\frac{\sqrt3}{2}$
$\cos 30^\circ=\frac{\sqrt3}{2}$	$\sin 45^\circ=\frac{1}{\sqrt 2}$	$\cos 60^\circ=\frac{1}{2}$
$\tan 30^\circ=\frac{1}{\sqrt 3}$	$\tan 45^\circ=1$	$\tan 60^\circ=\sqrt3$

Tabell 2: Exakta värden på de trigonometriska funktionerna för några vinklar

Ovanstående vinklar kan förekomma i rätvinkliga trianglar. Den räta vinkeln är 90°; sedan måste de andra vinklarnas summa uppgå till 90°.

I många fall då man räknar med utgångspunkt från trianglar vill man bestämma en vinkel utifrån ett förhållande mellan två sidor. Då kommer de inversa trigonometriska funktionerna till pass, arcsin, arccos och arctan (för ett givet förhållande mellan aktuella sidor). OBS: på miniräknaren finns beteckningarna sin-1, cos-1 och tan-1. Vid skrift bör dock skrivsättet arc- användas, då det inte innebär någon tvetydighet mellan en negativ exponent och en invers funktion.

Jämför nedanstående tabell med Tabell 2:

$\arcsin \frac{1}{2}=30^\circ$	$\arcsin \frac{1}{\sqrt 2}=45^\circ$	$\arcsin \frac{\sqrt 3}{2}=60^\circ$
$\arccos \frac{\sqrt3}{2}=30^\circ$	$\arccos \frac{1}{\sqrt 2}=45^\circ$	$\arccos \frac{1}{2}=60^\circ$
$\arctan \frac{1}{\sqrt3}=30^\circ$	$\arctan 1=45^\circ$	$\arctan \sqrt 3=60^\circ$

Tabell 3: Några vinklar utifrån givna förhållanden mellan två sidor i en rätvinklig triangel

Ovanstående innebär sammantaget att känner man till ett förhållande mellan två sidor i en rätvinklig triangel så känner man också till dess vinklar, och vice versa. Detta gäller för alla rätvinkliga trianglar, inte enbart för dessa med vinklarna 30°, 45° och 60° (som jag tog som exempel efter att ha konstruerat dessa vinklar från en liksidig triangel med sidan 1. Vi kommer senare att hitta fler exakta värden för de trigonometriska funktionerna.

Jag hittade denna demonstration från Wolfram (läs om, och hämta, det program som används för att spela upp sådana demonstrationer här), som beräknar de exakta värdena på respektive förhållande som ges av en mängd olika vinklar.

Trigonometri i enhetscirkeln

Som vi vet så representeras inte alla vinklar i en rätvinklig triangel; de båda vinklarna som inte är räta kommer att vara mindre än 90°. Däremot så fungerar de trigonometriska funktionerna för större vinklar än så, så vi behöver utveckla definitionen för sinus, cosinus och tangens en smula. Vi gör det med hjälp av enhetscirkeln.

Bild 3: Enhetscirkel med inskriven triangel. Vad händer för värdet på tangens för vinkeln, när den närmar sig 90°? (Klicka på bilden för att komma till dess beskrivning med ursprungs- och licensinformation)

I ovanstående bild är den röda triangeln (ΔODC) inskriven i en cirkel med radien 1. Ur den ursprungliga definitionen av sinus, cosinus och tangens gäller att sinusvärdet för vinkeln x utgör höjden på triangeln medan cosinusvärdet utgör basen på triangeln. För att få tangensvärdet är man tvungen att bygga på konstruktionen med den gula triangeln (ΔOAB), där tangensvärdet utgör denna triangelns höjd (lägg märke till vad som händer med denna höjd allteftersom vinkeln närmar sig 90°; vad skulle det innebära för ”värdet” av tan 90°?). Eller ett bättre sätt att se det på: sinusvärdet utgör y-koordinaten för punkten D och cosinusvärdet utgör dess x-koordinaten.

I nedanstående Wolfram-demonstration finns en enhetscirkel där vinkeln kan varieras runt hela cirkeln. Notera vad som händer med periferipunktens koordinater när den dras genom varvet.

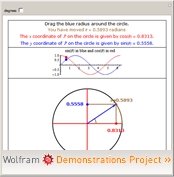
Vi ser hur ”visaren” tillsammans med sin höjd och del av x-axeln formar en triangel som dras runt över de olika kvadranterna i koordinatsystemet. På detta vis utökas definitionen för sinus, cosinus och tangens.

Slutligen vill jag även få med nedanstående bild, som åskådliggör hur de trigonometriska värdena hänger ihop med vinklarna:

Enhetscirkel med olika vinklar markerade. Observera symmetrin i koordinaterna för de olika vinklarna. (Klicka på bilden för att komma till dess beskrivning med ursprungs- och licensinformation)

Vi ser att sinusvärdena är parvis detsamma för t ex 30° och 150° respektive 45° och 135°. Symmetrin ger att summan av de vinklar med samma sinusvärde är 180° då vinklarna ligger i första och andra kvadranten av enhetscirkeln. (Vi kallar denna slutsats för [1])

Vi ser också att sinusvärdet är parvis detsamma för t ex 330° och 210° respektive 300° och 240°. Liksom att cosinusvärdet är parvis detsamma för t ex 30° och 330° respektive 60° och 300°. Kan någon enkel regel formuleras för dessa iakttagelser som grundar sig på cirkelns symmetri?

Lösningen på dessa symmetriska problem är att introducera negativa vinklar. Med utgångspunkt från 0° skapar vi positiva vinklar om visaren vrids moturs och negativa om den vrids medurs. Det innebär t ex att 330° = -30° och att 300° = -60°. Med utgångspunkt från detta kan vi nu titta på sinus- och cosinusvärden för några vinklar.

Vi noterade ovan att sin 330° = sin 210°. Om vi skriver om sin 330° = sin (-30°) gäller att de båda vinklarnas summa blir 210° + (-30°) = 180°. Slutsatsen blir att [1] gäller för vinklar i hela cirkeln.

På motsvarande sätt kan konstateras fler regler. Nedanstående tabell sammanfattar några av dem.

$\sin(180^\circ-v)=\sin v$	$\cos(180^\circ-v)=-\cos v$
$\sin(90^\circ-v)=\cos v$	$\cos(90^\circ-v)=\sin v$
$\sin(-v)=-\sin v$	$\cos (-v)=\cos v$

Tabell 4: Några samband mellan vinklar applicerade på trigonometriska funktioner

Ovanstående samband, som som sagt erhålls ur enhetscirkeln, är nyttiga verktyg vid trigonometrisk ekvationslösning.

Exempel på användning av samband

Lös ekvationen

$\cos v=0.5$

i det intervall där vinkeln v ligger mellan 0° och 360°.

Lösning: Man kan antingen se ekvationen som att den ger en vinkel i en triangel med ett av sina sidförhållanden = 0.5 eller som att den ger en vinkel i enhetscirkeln där ”visarens” projektion i x-led är 0.5. Genom att minnas sambanden mellan längdförhållanden och vinklar i Tabell 1 (eller genom att slå på miniräknaren) erhålls

$v=\arccos 0.5=60^\circ$

Detta är en lösning i intervallet (den svarar mot vinkeln i triangeln med ett av sina sidförhållanden på 0.5). Enligt enhetscirkeln, och Tabell 4, vet vi att det finns ytterligare en lösning, nämligen

$v=\arccos 0.5=-60^\circ=300^\circ$

Så den fullständiga lösningen på ekvationen, i det givna vinkelintervallet, är

$v_1=60^\circ$ och $v_2=300^\circ$

Avsnitt och rekommenderade uppgifter i boken

I läroboken Origo D motsvarar detta avsnitt 3.1, med start på sid. 90. Tidsplanen för detta avsnitt är lektionerna 16/5, 17/5 och 20/5. Några rekommenderade uppgifter:

3301, 02, 05, 07, 08, 09, 12, 14, 15, 16, 17, 18, 20, 22, 23, 24, 25, 26, 27, 29, 30, 31, 32, 33, 34, 35 och 36

4 reaktioner till “Trigonometri i enhetscirkeln och i rätvinkliga trianglar”

Pingback: Att utföra beräkningar i trianglar som ej är rätvinkliga | ξ-Blog
Pingback: Trigonometriska ekvationer | ξ-Blog
skrattja skriver:

6 november, 2014 kl. 17:00

din enhetscirkel är fel, 45 grader är 1/sqrt2 inte 2/sqrt2

Svara
1. Nikodemus skriver:
  
  9 november, 2014 kl. 22:00
  
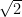  Nej, den är inte fel. Däremot framgår det att sinus- respektive cosinusvärdet av 45°= $\frac{\sqrt{2}}{2}$ , och det är samma sak som $\frac{1}{\sqrt{2}}$ . Kolla på en miniräknare, eller förläng den senare divisionen med $\sqrt{2}$ .
  
  Svara