Som lärare får jag ibland frågor om hur ”man kan känna till talet π med så många decimaler?” och hur ”det kommer sig att arean för en cirkel räknas ut med formeln \(A=\pi r^2\)?”. De flesta känner till att \(\pi\approx 3.14\), att det har något med cirklar att göra och kanske också att dess decimalantal går mot oändligheten. Som i så många andra fall finns inga enkla förklaringar i en ”one-liner”, men jag försöker mig på en sammanfattning nedan.
Innan det vill jag bara ange ett par rekord (vid tidpunkten för detta inläggs publicering) som har med π att göra:
- Världsrekordet i memorering av siffror i talet π: 70 030 stycken.
- Antal beräknade siffror i π med dator: 50 000 000 000 000
(50 biljoner) stycken.
Värdet på π – Arkimedes approximation
Talet pi (π) är fascinerande. Det är, i all sin enkelhet, förhållandet mellan en cirkels omkrets och dess diameter. En godtycklig cirkels omkrets dividerat med dess diameter är π. Alltid. Talet är irrationellt, det betyder att det inte kan skrivas som en kvot mellan två heltal. Det går att komma nära ett värde på π genom att inskriva och omskriva en cirkel med regelbundna polygoner. Den inskrivna polygonens omkrets ger en undre gräns för värdet på π och den omskrivna polygonens omkrets ger en övre. Arkimedes (287 – 212 f.kr.) utförde beräkningar enligt denna modell, och han kom så långt som till en 96-hörning som utvecklades enligt nedanstående mönster (Arkimedes utvecklade polygonerna från 6- till 12- till 24- till 48- till 96-hörning).
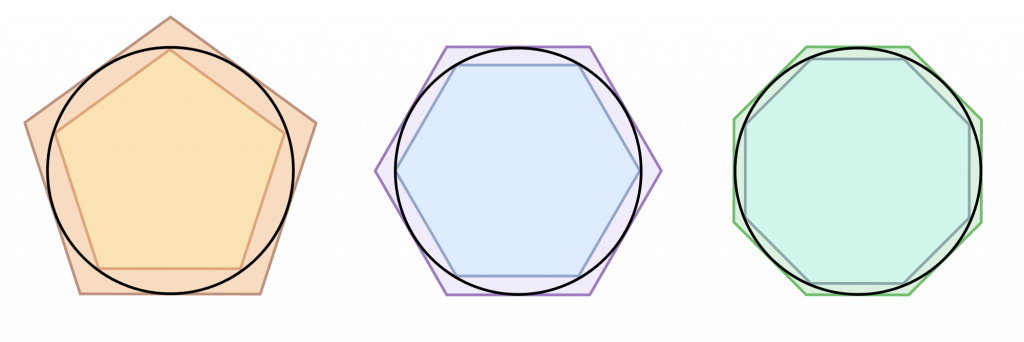
Med en 96-hörning erhålls en undre begränsning av π på \(\frac{223}{71}\) och en övre begränsning på \(\frac{22}{7}\). Därmed hade Arkimedes uttryckt värdet på π med felmarginalen \(\pm 1/1000\).
Även om det går att göra nog så goda approximationer med dylika geometriska metoder erbjuder den matematiska analysen (som bygger på inifinitesimalkalkyl, dvs derivator och integraler) större möjligheter att komma godtyckligt långt i approximationen av värdet på π. Sådana metoder började utvecklas under 1700-talet, runt 2000 år efter Arkimedes tid. Lite längre ned i inlägget påvisar jag en sådan analytisk metod, men först: arean för en cirkel.
Arean för en cirkel
Även om π dyker upp på många ställen inom matematik och sannolikhet är nog den första tillämpningen som elever stöter på när omkrets och area på cirklar ska beräknas. En av π:s definitioner (det finns flera) är förhållandet mellan omkrets (O) och diameter (d) på en cirkel, så ur det följer att omkretsen beräknas enligt \(O=\pi d\). Men att den dyker upp i formeln för arean av cirkel kanske kan tyckas lite märkligt.
Det går att troliggöra geometriskt med nedanstående figur till vänster. Ju fler sektorer som cirkeln delas upp i, desto bättre blir approximationen, när antalet går mot oändligheten går approximationen av cirkelns area mot likhet. Det hela syns geometriskt när sektorerna omorganiseras i en figur som blir mer och mer lik en rektangel. Höjden i denna är radien och längden är halva omkretsen, \(\pi r\).
Ett annat sätt att troliggöra formeln för cirkelns area (\(A=\pi r^2\)) är att göra tunna ringar inne i en cirkel, se figur ned till höger. Ju tunnare dessa ringar är, desto bättre approximeras de med en rektangel i samband med att ringen ”rätas ut”. Arean på en sådan ring approximeras bättre och bättre (då tjockleken går mot noll) av \(A_{\text{ring}}\approx (2\pi \cdot \,\mathrm{d}t)\). Hela cirkelns area erhålls då genom att summera alla dessa tunna ringars area som kan tänkas inne i cirkeln; när tjockleken går mot noll och antalet går mot oändligheten erhålls arean som nedanstående integral.
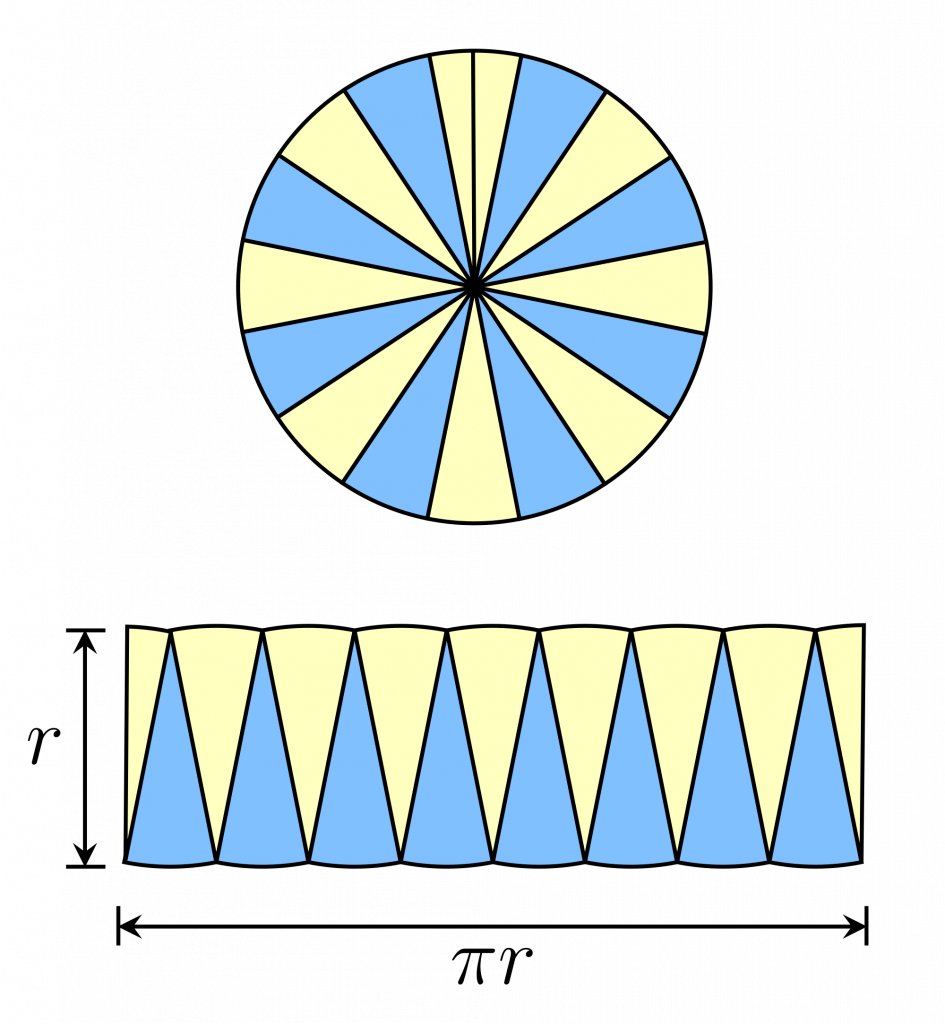
När antalet sektorer i cirkeln ökar kan de arrangeras om så att figuren blir mer och mer lik en rektangel. 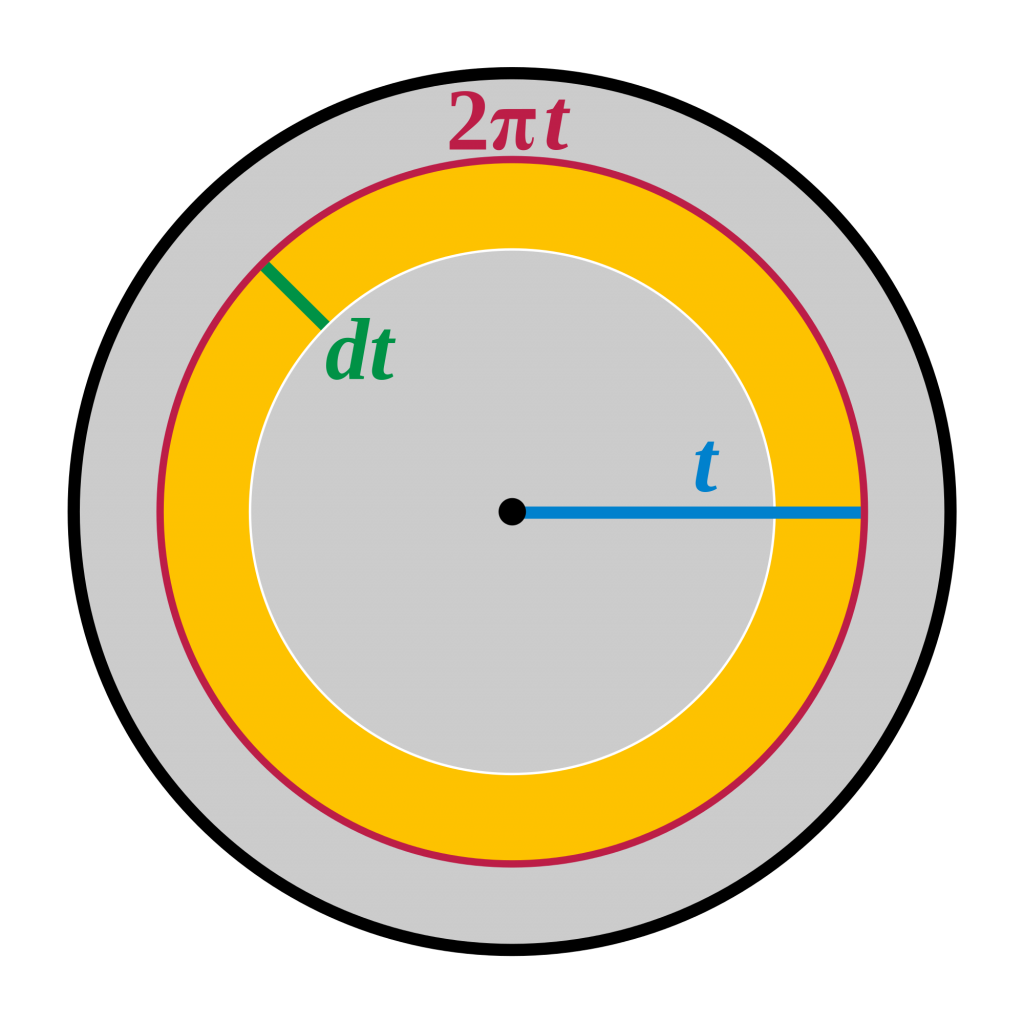
Det går även att integrera fram arean genom att summera de infinitesimalt smala ringarnas area.
\(A=\displaystyle\int_0^r 2\pi\,\mathrm{d}t=\pi r^2\)
Värdet på π, en serieutveckling
Hur kan då derivator och integral vara verktyg för att beräkna ett närmevärde på π? Jo, man kan använda Taylorutveckling. Vi börjar med att utveckla funktionen \(1/(1+u)\) runt \(u=0\), och hanterar resultatet enligt följande:
\(\displaystyle\frac{1}{1+u}=1-u+u^2-u^3+u^4-u^5+…\)
Nu ansätts \(\displaystyle u=x^2\):
\(\displaystyle\frac{1}{1+x^2}=1-x^2+x^4-x^6+x^8-x^{10}+…\;\;\;\;\;\;\;\;\;(1)\)
Eftersom \(\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(\arctan x)=\frac{1}{1+x^2}\), så gäller enligt (1)
\(\arctan y=\displaystyle\int_0^y\frac{\mathrm{d}x}{1+x^2}=y-\frac{y^3}{3}+\frac{y^5}{5}-\frac{y^7}{7}+…\)
Slutligen ansätts \(y=1\). Eftersom det är känt att \(\displaystyle\arctan{1}=\frac{\pi}{4}\) så gäller:
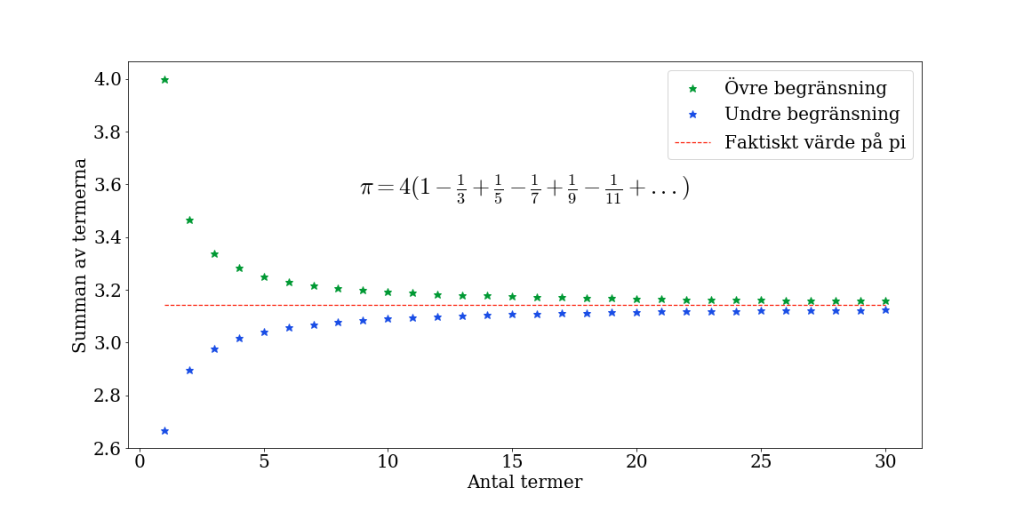
\(\displaystyle\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+…\)
Denna serie kallas för Leibniz formel för π.
Några av ovanstående begrepp tas inte upp på gymnasiet. Taylorutveckling går ut på att en funktion approximeras med hjälp av dess derivator i stigande ordning (värdet på dess förstaderivator, andraderivator osv) i en punkt. Ju fler derivator som används, desto bättre blir approximationen.
Derivatan för arctan-funktionen tas inte heller upp i gymnasiet, men den intresserade kan utgå från denna härledning på sajten proofwiki.
Att \(\tan\frac{\pi}{4}=1\) tas i alla fall upp i gymnasiet!
Man kan få en uppfattning om hur serien närmar sig \(\pi\) i följande graf, som visar värdet på summan beroende på antalet termer som summeras.
π i andra sammanhang
Det finns en uppsjö av andra sammanhang där π kommer upp; mer eller mindre väntat. Spellistan på YouTube nedan, från 3blue1brown, ger några exempel på sådana fall.

