En uppgift i en lärobok i Matematik 5 lyder något i stil med: Det finns tre bägare, A, B och C, som vardera innehåller fem blå och en röd kula. Man på måfå tar en kula ur bägare A och placerar i B, därefter på måfå tar en kula ur B för att placera i C.
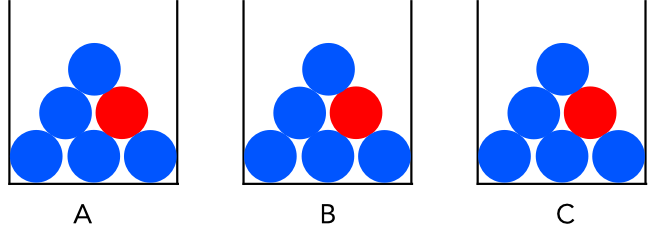
Efter dessa förflyttningar, beräkna sannolikheten att en slumpvis vald kula i bägare C är röd.
Den lösningsgång som jag föreslår är titta vilka möjliga utfall, och sannolikheterna för dessa, i respektive bägare efter alla drag.
Antal röda kulor i bägare | Sannolikhet
A B C | för utfall
----- ----- ----- ---------———-
0 2 1 | 1/6 * 5/7
0 1 2 | 1/6 * 2/7
1 1 1 | 5/6 * 6/7
1 0 2 | 5/6 * 1/7
Därefter är det bara att räkna sannolikheten för att den dragna kulan ur bägare C ska vara röd i respektive fall. Enligt additionsprincipen (det är exklusiva utfallsmöjligheter) ska dessa sannolikheter sedan adderas för att få den totala sannolikheten. Detta görs enligt
$$P_{\mathrm{röd}}=\frac{1}{7}\cdot\frac{1}{6}\cdot\frac{5}{7}+\frac{2}{7}\cdot\frac{1}{6}\cdot\frac{2}{7}\\+\frac{1}{7}\cdot\frac{5}{6}\cdot\frac{6}{7}+\frac{2}{7}\cdot\frac{5}{6}\cdot\frac{1}{7}=\frac{1}{6}$$