Etikett: mathematics

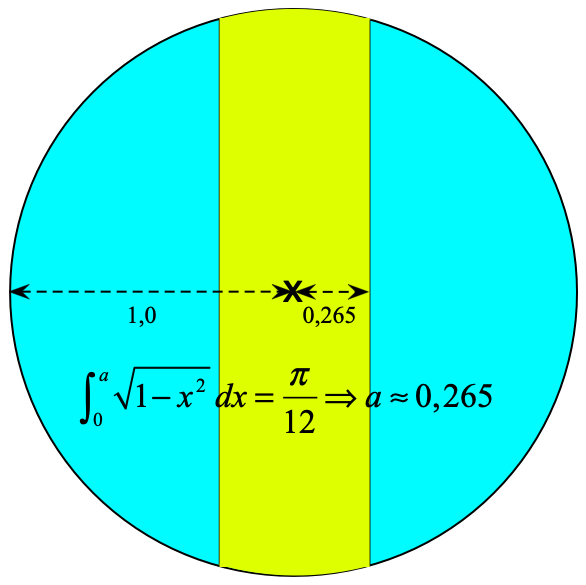
Cirkelns geometri gör att det inte alltid blir helt lätt att avgöra hur stor andel som är utskuren. Skulle man t ex dela på en pizza på tre så är jag rädd för att de som fått den gula delen i bilden nedan kommer att känna sig förfördelad. Dessutom är det en större andel kant i ytterdelarna, så snitten kanske behöver läggas ytterligare in mot mitten för ultimat rättvisa.

Lösningen på problemet är nog att beställa en större pizza. Om pizzans diameter ökar från 30 cm till 35 cm ökar dess area med 36 %.

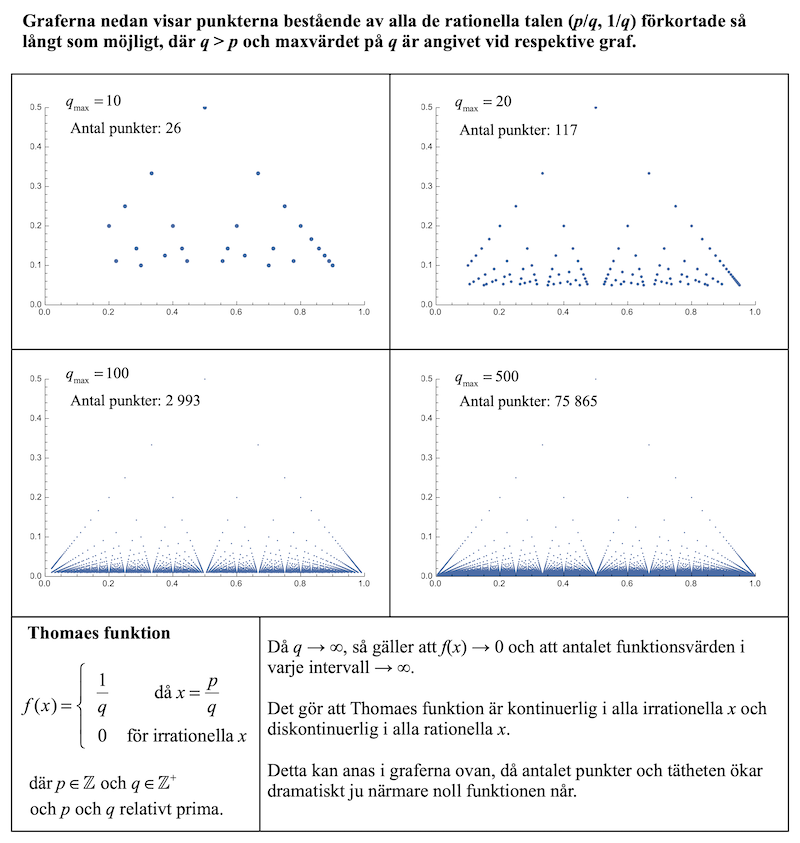
För den som vill evaluera integralen i bilden ovan analytiskt så finns substitutionen som måste göras här.

Jag läser om Thomaes funktion. Det är en funktion som är diskontinuerlig överallt utom i de irrationella talen. Jag var inte bekant med funktionen sedan mina tidigare studier (inte vad jag minns, iallafall), och det visade sig bli en tillfredsställande bekantskap. Den går ut på att när man stoppar in ett rationellt tal i funktionen så får den ett värde som är skilt från noll. Stoppar man däremot in ett irrationellt tal så är funktionsvärdet definierat till noll. Sedan låter man funktionen operera på hela mängden av rationella tal. En del av resultatet syns i nedanstående bildserie.

Kod i Mathematica (som är snodd härifrån); denna genererar ovanstående bilder:

maxq = 100;
fracs = Table[p/q, {q, 2, maxq}, {p, 2, q}] // Flatten // 
   DeleteDuplicates;
pq = {#, 1/Denominator@#} & /@ fracs;

ListPlot[pq, PlotRange -> {{0, 1}}]

Kan man inte få nog av märkliga funktioner så rekommenderar jag att läsa om Dirichlets funktion, som faktiskt inte är kontinuerlig någonstans, eller Weierstrass funktion som är kontinuerlig överallt men som inte är deriverbar någonstans.